Contents

Scalars:

x=2

x*3

x =

     2


ans =

     6

Vectors/matrices:

x=[1 2 3; 4 5 6; 7 8 9]

x(1,1) %returns 1st row, 1st column

x(1,1:2) %returns 1st row, columns 1 through 3

x(1,:) %returns the entire first row

x(1,3)= x(end, end) %assings a new value to position (1,3)

x*x %performs matrix multiplication

x.*x %performs element-by-element multiplication

%The "list notation" can also be used to assign values. We could have
%written the first line as x=[1:3; 4:6; 7:9]

x =

     1     2     3
     4     5     6
     7     8     9


ans =

     1


ans =

     1     2


ans =

     1     2     3


x =

     1     2     9
     4     5     6
     7     8     9


ans =

    72    84   102
    66    81   120
   102   126   192


ans =

     1     4    81
    16    25    36
    49    64    81

Conditional Indexing: Your new best friend

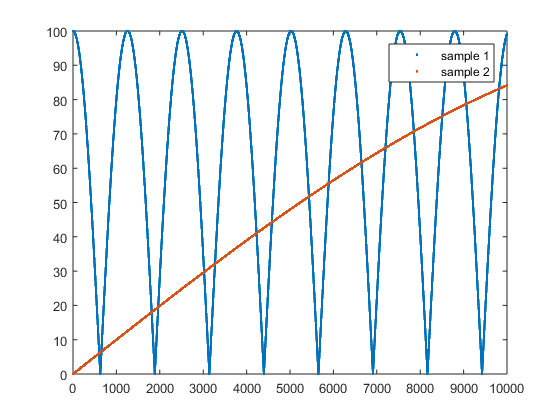
clear all
%We have some data as a function of time for two samples:
time=[1:10000];
sample1=abs(100*cos(time/400));
sample2=100*sin(time/10000);

figure(1)
plot(time,sample1,'.',time,sample2,'.')
legend({'sample 1' 'sample 2'})

Conditional indexing part 2

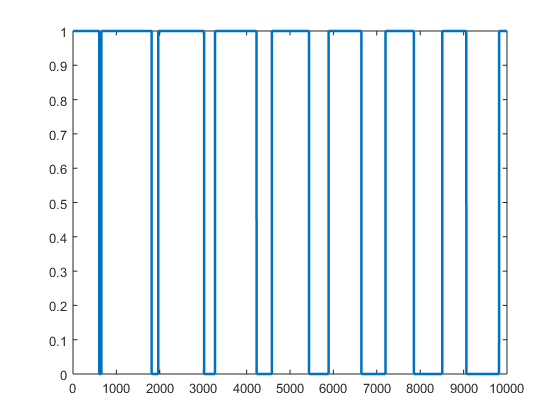
figure(2)
plot(sample1>sample2,'linewidth',2)

%What if we're interested only in data where sample1 is greater than sample 2?
%Instead of simply using row/column indexing, we can input conditions
tic

%get all values of the variosu vectors for indecies where the value of
%sample1 is higher than sample 2.
x=time(sample1>sample2);
y=sample1(sample1>sample2);
y2=sample2(sample1>sample2);
t1=toc;



%here is how you'd typically do this in C++/java/fortran/etc
%This method will still give the same results in Matlab, but is MUCH slower
tic
j=1;
for i=1:10000
    if sample1(i)>sample2(i)
        xif(j)=time(i);
        yif(j)=sample1(i);
        yif2(j)=sample2(i);
        j=j+1;
    end
end
t2=toc;

conditional indexing part 3

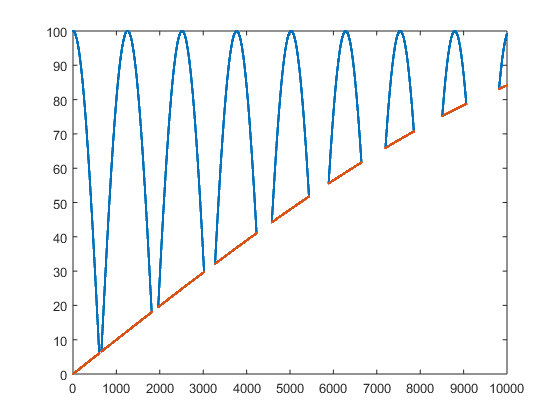
figure(3)
plot(x,y,'.',x,y2,'.')
ylim([0 100])
xlim([0 10000])

sprintf('Conditional indexing method took %0.2g seconds',t1)
sprintf('For loop and if statement method took %0.2g seconds',t2)
sprintf('Conditional indexing is %0.2g times faster',t2/t1)

ans =

Conditional indexing method took 0.00075 seconds


ans =

For loop and if statement method took 0.03 seconds


ans =

Conditional indexing is 40 times faster

Structures and Properties

clear all
%In matlab, you can also create structures that contain many different
%types of data.  This is useful in some situations and is used extensively
%by MTEX.

%Here we set up a structure called Sample.  Each sample has 4 properties:
%material, type, data, and rate
sample.material='Zircaloy-2';
sample.type='tensile';
sample.data=0:0.2:5;
sample.rate=1e-4;

Structures and Properties 2

%Like regular variables, structures can be made into arrays: Let's add a
%second entry to sample:
sample(2).material='Excel';
sample(2).type='compression';
sample(2).data=0:-0.2:-5;
sample(2).rate=1e-5;

Samples and Properties 3

%We can use conditional indexing on structures too!
%Let's say we wanted to find samples that had a rate of 1e-5

x=sample([sample.rate]==1e-5);

%note that we neeed to use square brackets to turn our structure output
%into something that can be directly compared to a value.  This is just an
%odd Matlab quirk.

Published with MATLAB® R2015a